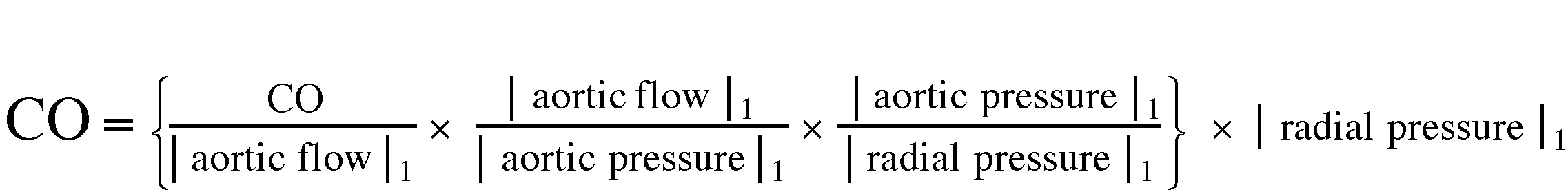
The new method is based upon the first harmonic of the blood pressure waveform. Advantages of using the lowest frequency component of the waveform are that at low frequencies:
In the following equation |…|1 indicates 'the modulus of the first harmonic', ZAII is the aortic input impedance, and TA_RA is the transfer function relating aortic to radial artery pressure. By definition:
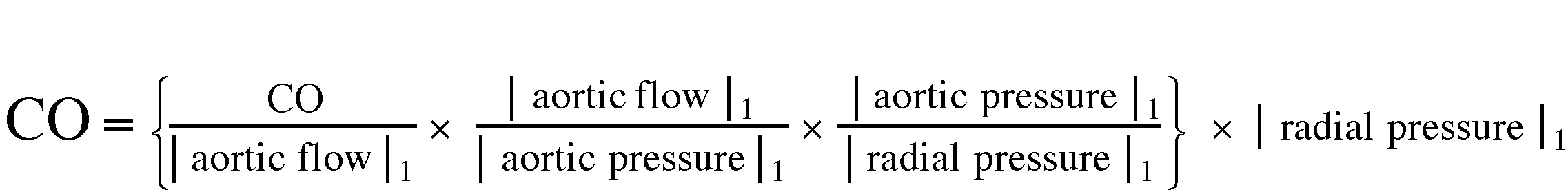
This can be restated as:

This equation arises from the definition of the various terms. It allows us to split one big problem (relating |radial pressure|1 to cardiac output) into 3 smaller problems. Now we need to estimate -
A scheme for the algorithm is shown in a figure, which corresponds to the text below (start at the bottom of the figure).
Aorta-Radial Pressure Transfer - TA_RA
This is required to estimate the modulus and phase of aortic pressure. The relationship has previously been determined by other workers. The heart rate (frequency of the first harmonic) is used in the calculation. The equations are approximations for use at low frequencies (<1.5Hz). We have designed the algorithm for use with radial (or brachial) artery pressure but aortic pressure could also be used if these equations are omitted. We do not recommend use with abdominal aortic or femoral artery pressure at this timeThe most important sites of wave reflection with respect to aortic input impedance are the vascular beds of the trunk (Karamanoglu et al. 1994).
Changes in the reflection coefficient of these beds would be expected to change the relationship between the pressure in the ascending aorta and that in the abdominal aorta (as well as arteries distal to this). For this reason the algorithm should be used with arterial pressure obtained from the upper limb
Modulus of Aortic Input Impedance - |ZAII|
Aortic input impedance varies markedly with changes in aortic pulse wave velocity and changes in wave reflection from vascular beds. Reduction in wave reflection causes the modulus of the aortic input impedance (ZAII) to fall (at low frequencies). The phase difference between aortic pressure and aortic flow (this is the phase of the aortic input impedance - phase(ZAII)) also diminishes.
Karamanoglu et al used a computer model to calculate aortic input impedance with different pulse wave velocities and different peripheral reflection coefficients. We found a formula that predicts | ZAII | to within 5% from the pulse wave velocity and the phase(ZAII), for frequencies less than 2 Hz. The aortic cross-sectional area is also required to convert ‘velocity impedance’ to ‘volumetric impedance’.
Pulse wave velocity and aortic area are predicted from mean arterial pressure and also the age and sex of the patient, using the relationships described by Langwouters et al. (1984). phase(ZAII) is required for the calculation – this is the difference between phase of the aortic pressure (which has already been found) and the phase of aortic flow (which is found below) - see equations.
Aortic Flow - CO/|aortic flow|1
It is assumed that there is no aortic flow during diastole (i.e. the aortic valve is competent). It is also assumed that the flow profile during systole remains constant, with the shape relative to the systolic time interval remaining unchanged. If these conditions are met then CO/|aortic flow|1 and the f(aortic flow)1 depend upon (ejection duration)/(cycle duration) alone. We developed equations from a flow profile that was considered to be typical.
Calibration
Calibration is required because absolute values of aortic area are variable (although the changes with arterial pressure are easier to predict). An indicator dilution method such as lithium dilution cardiac output is minimally invasive and could be used for this purpose.
Clinical Use
For brief details of its clinical validation please click here.