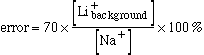The membrane of the lithium electrode is selectively permeable to lithium ions. The internal fill provides a constant ionic environment on the inside of the membrane. If the lithium concentration on the outside of the membrane changes this will alter the diffusion gradient for lithium across the membrane. There is no net movement of lithium ions through the membrane since it is not permeable to anions (so, for example, chloride ions cannot pass through). As no current can pass in the external measuring circuit, a potential difference is produced across the membrane. This is proportional to the logarithm of the ratio of ion activities on the two sides, as described by the Nernst equation:
![]()
where R = gas constant
T = absolute temperature
F = Faraday's number
z = valency
ln = natural logarithm
The expression RT/zF simplifies to 26.21 so the equation can then be written
![]()
A doubling of the external ion concentration will produce a change in membrane potential of 18 mV.
The selectivity of the lithium membrane for lithium over sodium is relatively poor. Normally lithium is only present in trace amounts in the plasma, but plasma sodium is about 140 mM. This level of sodium activity alters the membrane potential, having an effect which is equivalent to that of 2 mM lithium. In this application a further modification of the Nernst equation is needed to take this into account.
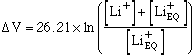
Where delta V is the change in voltage recorded as the sensor is moved from a solution which has an equivalent background lithium concentration [Li+EQ] to a sample of the same solution with additional lithium added. The equivalent background lithium concentration is due to sodium ions, against which the electrode membrane is not completely impermeable, as well as background lithium itself. [Other ions apart from sodium also affect the electrode potential but the effect is small enough to be ignored.]
![]()
where S represents the selectivity of the electrode against sodium.
The following equation is used to calculate the lithium concentration:

In plasma with a sodium concentration of 140 mM and no background lithium, a rise in lithium concentration to 1 mM produces a change in membrane potential of 10.5 mV. The background lithium equivalent is therefore 2.0 mM. Substituting this value in the previous equation gives S = 70.
In calculating the cardiac output from lithiuim dilution curves it is assumed that the background lithium concentration is zero. The previous equation shows that the calculated lithium dilution curve is proportional to the estimated equivalent background lithium concentration. The calculated cardiac output is inversely proportional to the integral of the primary curve. Therefore if there are no inaccuracies apart from the estimation of the equivalent background lithium concentration;
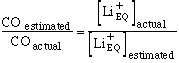
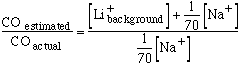
The percentage error incurred by assuming that no background lithium is present is therefore: